International Conference on Computer Vision (ICCV) 2023
(*: indicates joint first authors,order determined by coin flip)
Shape assembly aims to reassemble parts (or fragments) into a complete object, which is a common task in our daily life. Different from the semantic part assembly (e.g., assembling a chair's semantic parts like legs into a whole chair), geometric part assembly (e.g., assembling bowl fragments into a complete bowl) is an emerging task in computer vision and robotics. Instead of semantic information, this task focuses on geometric information of parts. As the both geometric and pose space of fractured parts are exceptionally large, shape pose disentanglement of part representations is beneficial to geometric shape assembly. In our paper, we propose to leverage SE(3) equivariance for such shape pose disentanglement. Moreover, while previous works in vision and robotics only consider SE(3) equivariance for the representations of single objects, we move a step forward and propose leveraging SE(3) equivariance for representations considering multi-part correlations, which further boosts the performance of the multi-part assembly. Experiments demonstrate the significance of SE(3) equivariance and our proposed method for geometric shape assembly.
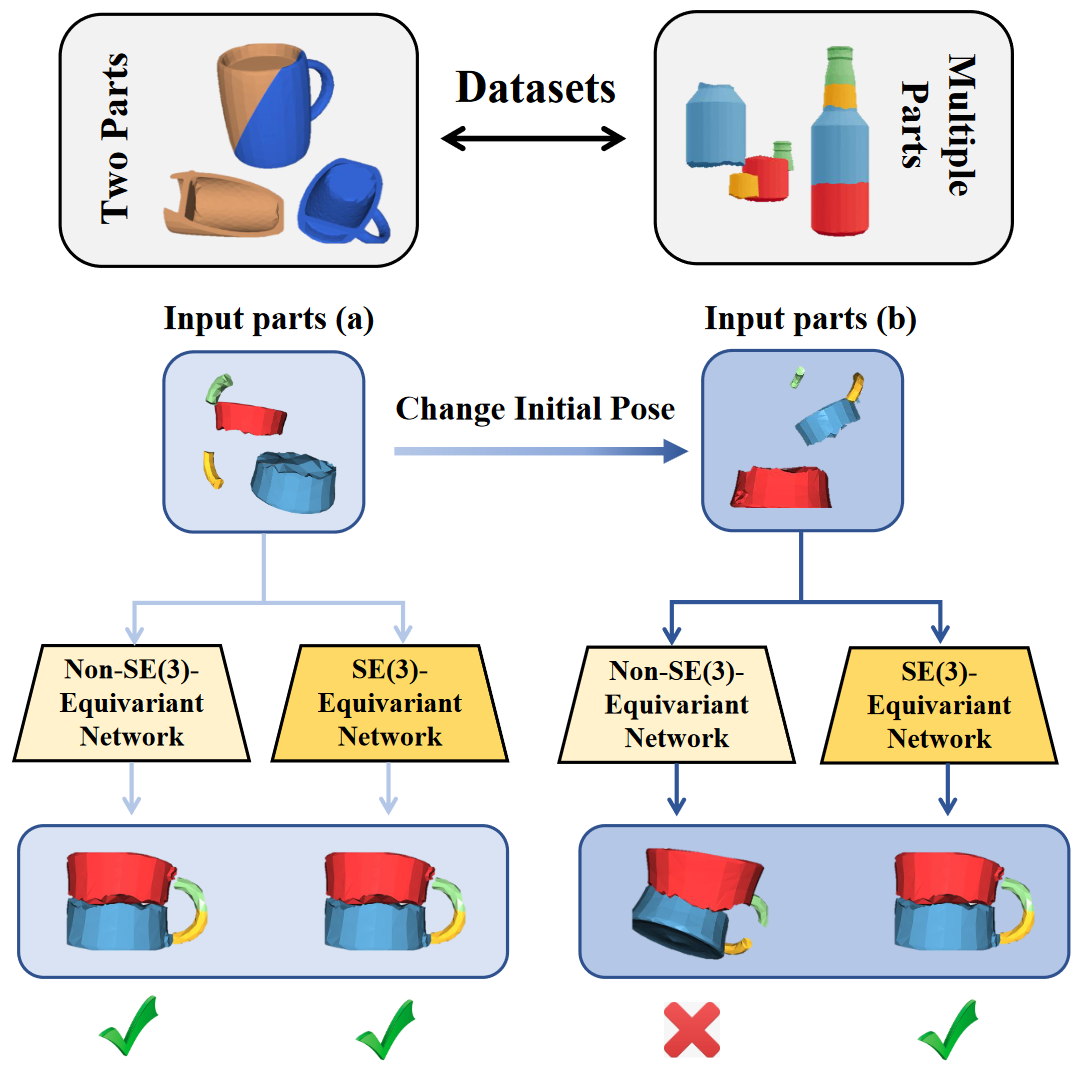
Figure 1. Geometric Shape Assembly aims to assemble different fractured parts into a whole shape. We propose to leverage SE(3) Equivariance for learning Geometric Shape Assembly, which disentangles poses and shapes of fractured parts, and performs better than networks without SE(3)-equivariant representations. |

Figure 2. Overview of our proposed framework Taking as input the point cloud of each part i, our framework first outputs the equivariant representation Fi and invariant representation Gi, computes the correlation between part i and each part j using the matrix multiplication of Fi and Gi, and thus gets each part's equivariant representation Hi with part correlations. The rotation decoder and the translation decoder respectively take H and decode the rotation and translation of each part. Additional constraints such as adversarial training and canonical point cloud reconstruction using G further improves the performance of our method. |
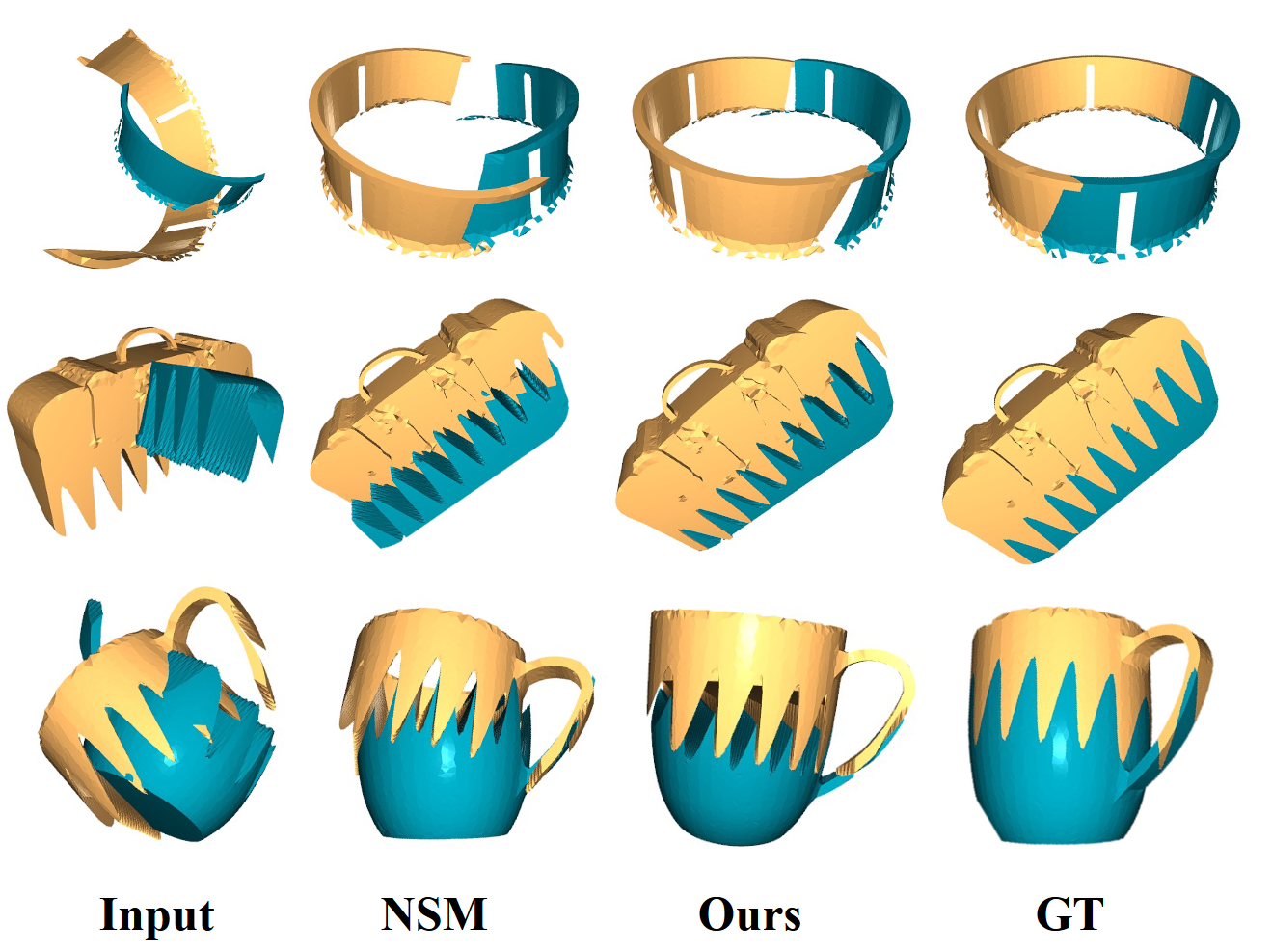
Figure 3. Qualitative results on Geometric Shape Mating dataset for two-part geometric shape assembly. We observe better pose predictions (especially rotation) than NSM(baseline). |
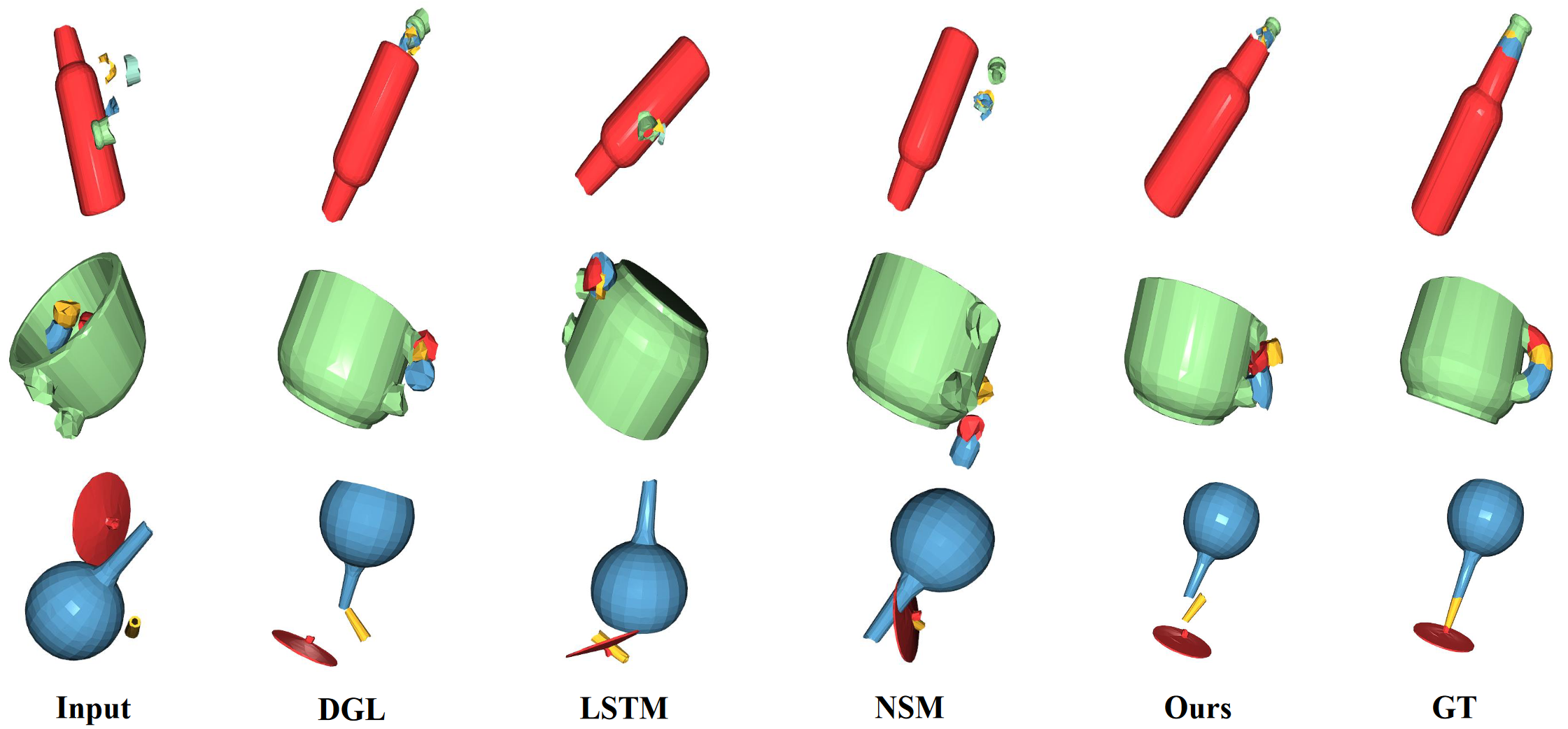
Figure 4. Qualitative results on Breaking Bad dataset for multi-part geometry shape assembly. |
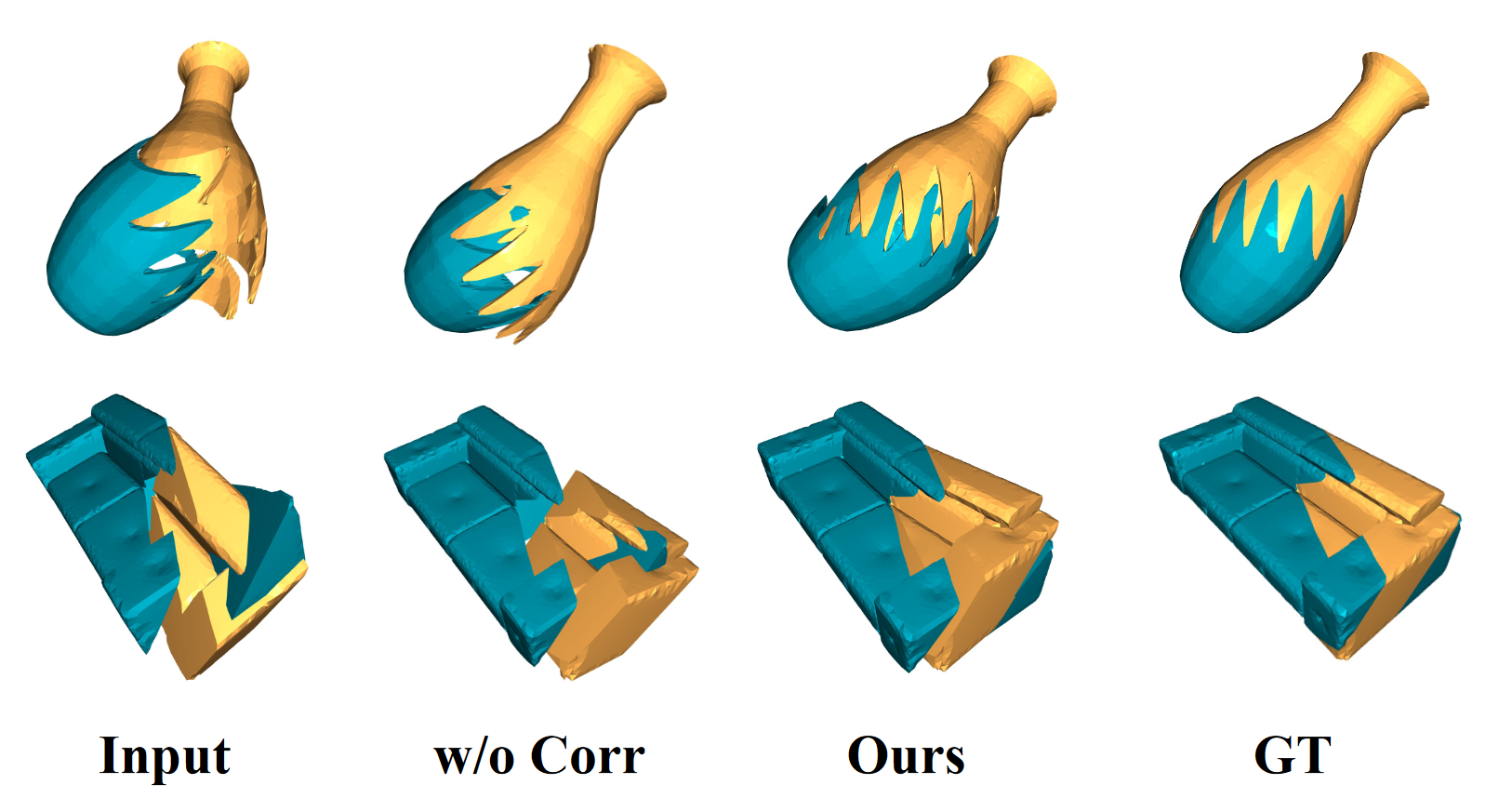
Figure 5. Qualitative results of our method with and without part correlation on Geometric Shape Mating dataset. We can see the parts match better when considering part correlations in part representations. |
If you have any questions, please feel free to contact Ruihai Wu at wuruihai_at_pku_edu_cn and Chenrui Tie at crtie_at_pku_edu_cn.